pacman::p_load(sf, tidyverse, funModeling, blorr, corrplot,
ggpubr, spdep, GWmodel, tmap, skimr, caret)In-Class Exercise 5
Setting the Scene
To build an explanatory model to discover factors affecting water point status in Osun State, Nigeria
Study area: Osun State, Nigeria
Data sets:
Osun.rds- a sf polygon data frame containing LGA boundaries of Osun StateOsun_wp_sf.rds- a sf point data frame containing water points within Osun State
Model Variables
Dependent variables: Water point status (i.e. functional/non-functional)
Independent variables:
distance_to_primary_road
distance_to_secondary_road
distance_to_tertiary_road
distance_to_city
distance_to_town
water_point_population
local_population_1km
usage_capacity
is_urban
water_source_clean
Note that the first 7 variables are continuous while the last 3 are categorical in nature.
Getting Started
In the code chunk below, p_load() of pacman package is used to install and load the following R packages into R environment.
Importing the Analytical Data
Appropriate data wrangling has been done on the two data sets involved, and we will import the transformed data of rds format.
Osun <- read_rds("data/Osun.rds")
Osun_wp_sf <- read_rds("data/Osun_wp_sf.rds")Next, we check on the proportion of values in status field in Osun_wp_sf, with TRUE representing the functional water points and FALSE representing the non-functional water points.
Osun_wp_sf %>%
freq(input = 'status')
status frequency percentage cumulative_perc
1 TRUE 2642 55.5 55.5
2 FALSE 2118 44.5 100.0The code chunks below creates an interactive point symbol map using functions of tmap package.
tmap_mode("view")
tm_shape(Osun) +
tmap_options(check.and.fix = TRUE) +
tm_polygons(alpha = 0.4) +
tm_shape(Osun_wp_sf) +
tm_dots(col = "status",
alpha = 0.6) +
tm_view(set.zoom.limits = c(9,12))tmap_mode("plot")Exploratory Data Analysis
The code chunk below displays the Summary Statistics with skimr package.
Osun_wp_sf %>%
skim()| Name | Piped data |
| Number of rows | 4760 |
| Number of columns | 75 |
| _______________________ | |
| Column type frequency: | |
| character | 47 |
| logical | 5 |
| numeric | 23 |
| ________________________ | |
| Group variables | None |
Variable type: character
| skim_variable | n_missing | complete_rate | min | max | empty | n_unique | whitespace |
|---|---|---|---|---|---|---|---|
| source | 0 | 1.00 | 5 | 44 | 0 | 2 | 0 |
| report_date | 0 | 1.00 | 22 | 22 | 0 | 42 | 0 |
| status_id | 0 | 1.00 | 2 | 7 | 0 | 3 | 0 |
| water_source_clean | 0 | 1.00 | 8 | 22 | 0 | 3 | 0 |
| water_source_category | 0 | 1.00 | 4 | 6 | 0 | 2 | 0 |
| water_tech_clean | 24 | 0.99 | 9 | 23 | 0 | 3 | 0 |
| water_tech_category | 24 | 0.99 | 9 | 15 | 0 | 2 | 0 |
| facility_type | 0 | 1.00 | 8 | 8 | 0 | 1 | 0 |
| clean_country_name | 0 | 1.00 | 7 | 7 | 0 | 1 | 0 |
| clean_adm1 | 0 | 1.00 | 3 | 5 | 0 | 5 | 0 |
| clean_adm2 | 0 | 1.00 | 3 | 14 | 0 | 35 | 0 |
| clean_adm3 | 4760 | 0.00 | NA | NA | 0 | 0 | 0 |
| clean_adm4 | 4760 | 0.00 | NA | NA | 0 | 0 | 0 |
| installer | 4760 | 0.00 | NA | NA | 0 | 0 | 0 |
| management_clean | 1573 | 0.67 | 5 | 37 | 0 | 7 | 0 |
| status_clean | 0 | 1.00 | 9 | 32 | 0 | 7 | 0 |
| pay | 0 | 1.00 | 2 | 39 | 0 | 7 | 0 |
| fecal_coliform_presence | 4760 | 0.00 | NA | NA | 0 | 0 | 0 |
| subjective_quality | 0 | 1.00 | 18 | 20 | 0 | 4 | 0 |
| activity_id | 4757 | 0.00 | 36 | 36 | 0 | 3 | 0 |
| scheme_id | 4760 | 0.00 | NA | NA | 0 | 0 | 0 |
| wpdx_id | 0 | 1.00 | 12 | 12 | 0 | 4760 | 0 |
| notes | 0 | 1.00 | 2 | 96 | 0 | 3502 | 0 |
| orig_lnk | 4757 | 0.00 | 84 | 84 | 0 | 1 | 0 |
| photo_lnk | 41 | 0.99 | 84 | 84 | 0 | 4719 | 0 |
| country_id | 0 | 1.00 | 2 | 2 | 0 | 1 | 0 |
| data_lnk | 0 | 1.00 | 79 | 96 | 0 | 2 | 0 |
| water_point_history | 0 | 1.00 | 142 | 834 | 0 | 4750 | 0 |
| clean_country_id | 0 | 1.00 | 3 | 3 | 0 | 1 | 0 |
| country_name | 0 | 1.00 | 7 | 7 | 0 | 1 | 0 |
| water_source | 0 | 1.00 | 8 | 30 | 0 | 4 | 0 |
| water_tech | 0 | 1.00 | 5 | 37 | 0 | 20 | 0 |
| adm2 | 0 | 1.00 | 3 | 14 | 0 | 33 | 0 |
| adm3 | 4760 | 0.00 | NA | NA | 0 | 0 | 0 |
| management | 1573 | 0.67 | 5 | 47 | 0 | 7 | 0 |
| adm1 | 0 | 1.00 | 4 | 5 | 0 | 4 | 0 |
| New Georeferenced Column | 0 | 1.00 | 16 | 35 | 0 | 4760 | 0 |
| lat_lon_deg | 0 | 1.00 | 13 | 32 | 0 | 4760 | 0 |
| public_data_source | 0 | 1.00 | 84 | 102 | 0 | 2 | 0 |
| converted | 0 | 1.00 | 53 | 53 | 0 | 1 | 0 |
| created_timestamp | 0 | 1.00 | 22 | 22 | 0 | 2 | 0 |
| updated_timestamp | 0 | 1.00 | 22 | 22 | 0 | 2 | 0 |
| Geometry | 0 | 1.00 | 33 | 37 | 0 | 4760 | 0 |
| ADM2_EN | 0 | 1.00 | 3 | 14 | 0 | 30 | 0 |
| ADM2_PCODE | 0 | 1.00 | 8 | 8 | 0 | 30 | 0 |
| ADM1_EN | 0 | 1.00 | 4 | 4 | 0 | 1 | 0 |
| ADM1_PCODE | 0 | 1.00 | 5 | 5 | 0 | 1 | 0 |
Variable type: logical
| skim_variable | n_missing | complete_rate | mean | count |
|---|---|---|---|---|
| rehab_year | 4760 | 0 | NaN | : |
| rehabilitator | 4760 | 0 | NaN | : |
| is_urban | 0 | 1 | 0.39 | FAL: 2884, TRU: 1876 |
| latest_record | 0 | 1 | 1.00 | TRU: 4760 |
| status | 0 | 1 | 0.56 | TRU: 2642, FAL: 2118 |
Variable type: numeric
| skim_variable | n_missing | complete_rate | mean | sd | p0 | p25 | p50 | p75 | p100 | hist |
|---|---|---|---|---|---|---|---|---|---|---|
| row_id | 0 | 1.00 | 68550.48 | 10216.94 | 49601.00 | 66874.75 | 68244.50 | 69562.25 | 471319.00 | ▇▁▁▁▁ |
| lat_deg | 0 | 1.00 | 7.68 | 0.22 | 7.06 | 7.51 | 7.71 | 7.88 | 8.06 | ▁▂▇▇▇ |
| lon_deg | 0 | 1.00 | 4.54 | 0.21 | 4.08 | 4.36 | 4.56 | 4.71 | 5.06 | ▃▆▇▇▂ |
| install_year | 1144 | 0.76 | 2008.63 | 6.04 | 1917.00 | 2006.00 | 2010.00 | 2013.00 | 2015.00 | ▁▁▁▁▇ |
| fecal_coliform_value | 4760 | 0.00 | NaN | NA | NA | NA | NA | NA | NA | |
| distance_to_primary_road | 0 | 1.00 | 5021.53 | 5648.34 | 0.01 | 719.36 | 2972.78 | 7314.73 | 26909.86 | ▇▂▁▁▁ |
| distance_to_secondary_road | 0 | 1.00 | 3750.47 | 3938.63 | 0.15 | 460.90 | 2554.25 | 5791.94 | 19559.48 | ▇▃▁▁▁ |
| distance_to_tertiary_road | 0 | 1.00 | 1259.28 | 1680.04 | 0.02 | 121.25 | 521.77 | 1834.42 | 10966.27 | ▇▂▁▁▁ |
| distance_to_city | 0 | 1.00 | 16663.99 | 10960.82 | 53.05 | 7930.75 | 15030.41 | 24255.75 | 47934.34 | ▇▇▆▃▁ |
| distance_to_town | 0 | 1.00 | 16726.59 | 12452.65 | 30.00 | 6876.92 | 12204.53 | 27739.46 | 44020.64 | ▇▅▃▃▂ |
| rehab_priority | 2654 | 0.44 | 489.33 | 1658.81 | 0.00 | 7.00 | 91.50 | 376.25 | 29697.00 | ▇▁▁▁▁ |
| water_point_population | 4 | 1.00 | 513.58 | 1458.92 | 0.00 | 14.00 | 119.00 | 433.25 | 29697.00 | ▇▁▁▁▁ |
| local_population_1km | 4 | 1.00 | 2727.16 | 4189.46 | 0.00 | 176.00 | 1032.00 | 3717.00 | 36118.00 | ▇▁▁▁▁ |
| crucialness_score | 798 | 0.83 | 0.26 | 0.28 | 0.00 | 0.07 | 0.15 | 0.35 | 1.00 | ▇▃▁▁▁ |
| pressure_score | 798 | 0.83 | 1.46 | 4.16 | 0.00 | 0.12 | 0.41 | 1.24 | 93.69 | ▇▁▁▁▁ |
| usage_capacity | 0 | 1.00 | 560.74 | 338.46 | 300.00 | 300.00 | 300.00 | 1000.00 | 1000.00 | ▇▁▁▁▅ |
| days_since_report | 0 | 1.00 | 2692.69 | 41.92 | 1483.00 | 2688.00 | 2693.00 | 2700.00 | 4645.00 | ▁▇▁▁▁ |
| staleness_score | 0 | 1.00 | 42.80 | 0.58 | 23.13 | 42.70 | 42.79 | 42.86 | 62.66 | ▁▁▇▁▁ |
| location_id | 0 | 1.00 | 235865.49 | 6657.60 | 23741.00 | 230638.75 | 236199.50 | 240061.25 | 267454.00 | ▁▁▁▁▇ |
| cluster_size | 0 | 1.00 | 1.05 | 0.25 | 1.00 | 1.00 | 1.00 | 1.00 | 4.00 | ▇▁▁▁▁ |
| lat_deg_original | 4760 | 0.00 | NaN | NA | NA | NA | NA | NA | NA | |
| lon_deg_original | 4760 | 0.00 | NaN | NA | NA | NA | NA | NA | NA | |
| count | 0 | 1.00 | 1.00 | 0.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | ▁▁▇▁▁ |
Note that some of the independent variables have many missing records, for example install_year has as many as 1144 records missing. Whereas some of the independent variables only have a few missing records, for example water_point_population and local_population_1km only have 4 records missing respectively.
The code chunk below is used to remove rows of those missing values from the independent variables.
Osun_wp_sf_clean <- Osun_wp_sf %>%
filter_at(vars(status,
distance_to_primary_road,
distance_to_secondary_road,
distance_to_tertiary_road,
distance_to_city,
distance_to_town,
water_point_population,
local_population_1km,
usage_capacity,
is_urban,
water_source_clean),
all_vars(!is.na(.))) %>%
mutate(usage_capacity = as.factor(usage_capacity))Correlation Analysis
The code chunk below is used to display a correlation plot of the independent variables.
Osun_wp <- Osun_wp_sf_clean %>%
select(c(7,35:39,42:43,46:47,57)) %>%
st_set_geometry(NULL)cluster_vars.cor = cor(
Osun_wp[,2:7])
corrplot.mixed(cluster_vars.cor,
lower = "ellipse",
upper = "number",
tl.pos = "lt",
diag = "l",
tl.col = "black")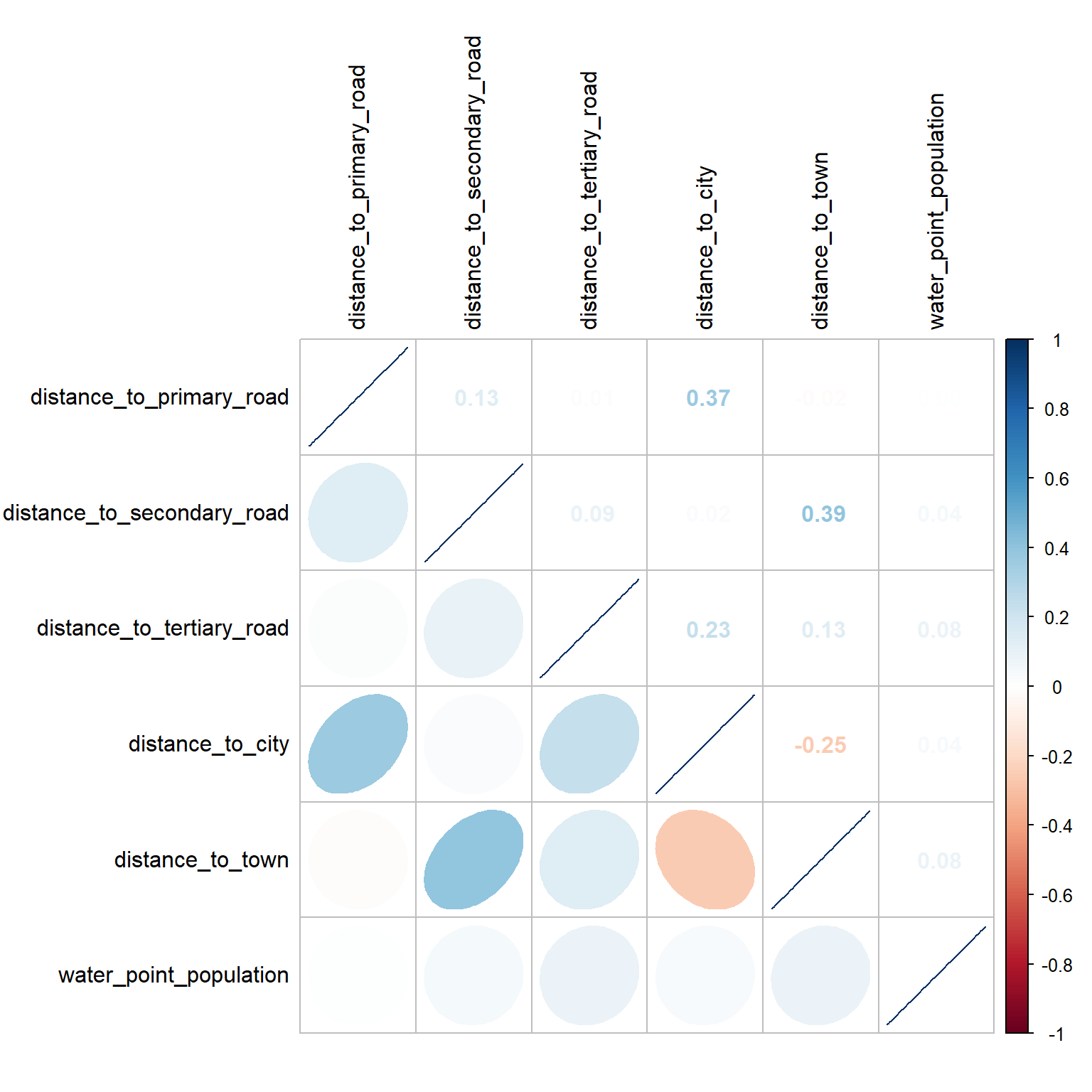
From the correlation output above, we can see that there are not any pairs of independent variables which are highly correlated (i.e. +/-0.8). Therefore, there is no sign of multicollinearity here.
Building Logistic Regression Models
model <- glm(status ~ distance_to_primary_road +
distance_to_secondary_road +
distance_to_tertiary_road +
distance_to_city +
distance_to_town +
is_urban +
usage_capacity +
water_source_clean +
water_point_population +
local_population_1km,
data = Osun_wp_sf_clean,
family = binomial(link = 'logit'))Instead of using typical R report, blr_regress() of blorr package is used.
blr_regress(model) Model Overview
------------------------------------------------------------------------
Data Set Resp Var Obs. Df. Model Df. Residual Convergence
------------------------------------------------------------------------
data status 4756 4755 4744 TRUE
------------------------------------------------------------------------
Response Summary
--------------------------------------------------------
Outcome Frequency Outcome Frequency
--------------------------------------------------------
0 2114 1 2642
--------------------------------------------------------
Maximum Likelihood Estimates
-----------------------------------------------------------------------------------------------
Parameter DF Estimate Std. Error z value Pr(>|z|)
-----------------------------------------------------------------------------------------------
(Intercept) 1 0.3887 0.1124 3.4588 5e-04
distance_to_primary_road 1 0.0000 0.0000 -0.7153 0.4744
distance_to_secondary_road 1 0.0000 0.0000 -0.5530 0.5802
distance_to_tertiary_road 1 1e-04 0.0000 4.6708 0.0000
distance_to_city 1 0.0000 0.0000 -4.7574 0.0000
distance_to_town 1 0.0000 0.0000 -4.9170 0.0000
is_urbanTRUE 1 -0.2971 0.0819 -3.6294 3e-04
usage_capacity1000 1 -0.6230 0.0697 -8.9366 0.0000
water_source_cleanProtected Shallow Well 1 0.5040 0.0857 5.8783 0.0000
water_source_cleanProtected Spring 1 1.2882 0.4388 2.9359 0.0033
water_point_population 1 -5e-04 0.0000 -11.3686 0.0000
local_population_1km 1 3e-04 0.0000 19.2953 0.0000
-----------------------------------------------------------------------------------------------
Association of Predicted Probabilities and Observed Responses
---------------------------------------------------------------
% Concordant 0.7347 Somers' D 0.4693
% Discordant 0.2653 Gamma 0.4693
% Tied 0.0000 Tau-a 0.2318
Pairs 5585188 c 0.7347
---------------------------------------------------------------Two of the variables distance_to_primary_road and distance_to_secondary_road are having p-value greater than 0.05, we should exclude these two variables later because they are not statistically significant.
In the code chunk below, blr_confusion_matrix() of blorr package is used to compute the confusion matrix of the estimated outcomes by using 0.5 as the cutoff value.
blr_confusion_matrix(model, cutoff = 0.5)Confusion Matrix and Statistics
Reference
Prediction FALSE TRUE
0 1301 738
1 813 1904
Accuracy : 0.6739
No Information Rate : 0.4445
Kappa : 0.3373
McNemars's Test P-Value : 0.0602
Sensitivity : 0.7207
Specificity : 0.6154
Pos Pred Value : 0.7008
Neg Pred Value : 0.6381
Prevalence : 0.5555
Detection Rate : 0.4003
Detection Prevalence : 0.5713
Balanced Accuracy : 0.6680
Precision : 0.7008
Recall : 0.7207
'Positive' Class : 1From the output, the overall Accuracy of the Logistic Regression Model is 0.6739 while the True Positive (0.7207) is greater than the True Negative (0.6154).
Building Logistic Regression Model - Excluding 2 variables
The code chunk below is used to compute the confusion matrix of the estimated outcomes for the LR model excluding 2 variables.
Model Overview
------------------------------------------------------------------------
Data Set Resp Var Obs. Df. Model Df. Residual Convergence
------------------------------------------------------------------------
data status 4756 4755 4746 TRUE
------------------------------------------------------------------------
Response Summary
--------------------------------------------------------
Outcome Frequency Outcome Frequency
--------------------------------------------------------
0 2114 1 2642
--------------------------------------------------------
Maximum Likelihood Estimates
-----------------------------------------------------------------------------------------------
Parameter DF Estimate Std. Error z value Pr(>|z|)
-----------------------------------------------------------------------------------------------
(Intercept) 1 0.3540 0.1055 3.3541 8e-04
distance_to_tertiary_road 1 1e-04 0.0000 4.9096 0.0000
distance_to_city 1 0.0000 0.0000 -5.2022 0.0000
distance_to_town 1 0.0000 0.0000 -5.4660 0.0000
is_urbanTRUE 1 -0.2667 0.0747 -3.5690 4e-04
usage_capacity1000 1 -0.6206 0.0697 -8.9081 0.0000
water_source_cleanProtected Shallow Well 1 0.4947 0.0850 5.8228 0.0000
water_source_cleanProtected Spring 1 1.2790 0.4384 2.9174 0.0035
water_point_population 1 -5e-04 0.0000 -11.3902 0.0000
local_population_1km 1 3e-04 0.0000 19.4069 0.0000
-----------------------------------------------------------------------------------------------
Association of Predicted Probabilities and Observed Responses
---------------------------------------------------------------
% Concordant 0.7349 Somers' D 0.4697
% Discordant 0.2651 Gamma 0.4697
% Tied 0.0000 Tau-a 0.2320
Pairs 5585188 c 0.7349
---------------------------------------------------------------blr_confusion_matrix(model_1, cutoff = 0.5)Confusion Matrix and Statistics
Reference
Prediction FALSE TRUE
0 1300 743
1 814 1899
Accuracy : 0.6726
No Information Rate : 0.4445
Kappa : 0.3348
McNemars's Test P-Value : 0.0761
Sensitivity : 0.7188
Specificity : 0.6149
Pos Pred Value : 0.7000
Neg Pred Value : 0.6363
Prevalence : 0.5555
Detection Rate : 0.3993
Detection Prevalence : 0.5704
Balanced Accuracy : 0.6669
Precision : 0.7000
Recall : 0.7188
'Positive' Class : 1From the output, this LR model has a slightly worse Accuracy of 0.6726 compared to that of the LR model with all variables included (0.6739). This is the common behaviour of the regression models that the model performance will be compromised when an independent variable is removed. In this case, since the difference in Accuracy is very minimal, we can conclude that the performance of the LR model is not really impacted when two independent variables are excluded.
Building Geographically Weighted Logistic Regression (GWLR) Models
Converting from sf to sp data frame
Osun_wp_sp <- Osun_wp_sf_clean %>%
select(c(status,
distance_to_primary_road,
distance_to_secondary_road,
distance_to_tertiary_road,
distance_to_city,
distance_to_town,
water_point_population,
local_population_1km,
usage_capacity,
is_urban,
water_source_clean)) %>%
as_Spatial()
Osun_wp_spclass : SpatialPointsDataFrame
features : 4756
extent : 182502.4, 290751, 340054.1, 450905.3 (xmin, xmax, ymin, ymax)
crs : +proj=tmerc +lat_0=4 +lon_0=8.5 +k=0.99975 +x_0=670553.98 +y_0=0 +a=6378249.145 +rf=293.465 +towgs84=-92,-93,122,0,0,0,0 +units=m +no_defs
variables : 11
names : status, distance_to_primary_road, distance_to_secondary_road, distance_to_tertiary_road, distance_to_city, distance_to_town, water_point_population, local_population_1km, usage_capacity, is_urban, water_source_clean
min values : 0, 0.014461356813335, 0.152195902540837, 0.017815121653488, 53.0461399623541, 30.0019777713073, 0, 0, 1000, 0, Borehole
max values : 1, 26909.8616132094, 19559.4793799085, 10966.2705628969, 47934.343603562, 44020.6393368124, 29697, 36118, 300, 1, Protected Spring Building Fixed Bandwidth GWR Model
Computing Fixed Bandwidth
bw.fixed <- bw.ggwr(status ~ distance_to_primary_road +
distance_to_secondary_road +
distance_to_tertiary_road +
distance_to_city +
distance_to_town +
is_urban +
usage_capacity +
water_source_clean +
water_point_population +
local_population_1km,
data = Osun_wp_sp,
family = "binomial",
approach = "AIC",
kernel = "gaussian",
adaptive = FALSE,
longlat = FALSE)bw.fixedgwlr.fixed <- ggwr.basic(status ~ distance_to_primary_road +
distance_to_secondary_road +
distance_to_tertiary_road +
distance_to_city +
distance_to_town +
is_urban +
usage_capacity +
water_source_clean +
water_point_population +
local_population_1km,
data = Osun_wp_sp,
bw = 2599.672,
family = "binomial",
kernel = "gaussian",
adaptive = FALSE,
longlat = FALSE) Iteration Log-Likelihood
=========================
0 -1958
1 -1676
2 -1526
3 -1443
4 -1405
5 -1405 From the output above, we can see that the AIC for the GWLR Model dropped to 4761.809 from 5684.357.
Model Assessment
Converting SDF into sf data frame
To assess the performance of the GWLR, we will first convert the SDF object into sf data frame by using the code chunk below.
gwr.fixed <- as.data.frame(gwlr.fixed$SDF)Next, we will label yhat values greater or equal to 0.5 into 1 and else 0. The result of the logic comparison operation will be saved into a field called most.
gwr.fixed <- gwr.fixed %>%
mutate(most = ifelse(
gwr.fixed$yhat >= 0.5, T, F))gwr.fixed$y <- as.factor(gwr.fixed$y)
gwr.fixed$most <- as.factor(gwr.fixed$most)
CM <- confusionMatrix(data = gwr.fixed$most, reference = gwr.fixed$y)
CMConfusion Matrix and Statistics
Reference
Prediction FALSE TRUE
FALSE 1824 263
TRUE 290 2379
Accuracy : 0.8837
95% CI : (0.8743, 0.8927)
No Information Rate : 0.5555
P-Value [Acc > NIR] : <2e-16
Kappa : 0.7642
Mcnemar's Test P-Value : 0.2689
Sensitivity : 0.8628
Specificity : 0.9005
Pos Pred Value : 0.8740
Neg Pred Value : 0.8913
Prevalence : 0.4445
Detection Rate : 0.3835
Detection Prevalence : 0.4388
Balanced Accuracy : 0.8816
'Positive' Class : FALSE
The overall Accuracy now improves to 0.8837, meaning that the GWLR Model geographically managed to improve greatly, from the LR’s Accuracy of 0.6739. Sensitivity and Specificity also improved to 0.8628 and 0.9005 respectively.
Building Geographically Weighted Logistic Regression Model - Excluding 2 variables
The code chunk below is used to compute the confusion matrix of the estimated outcomes for the GWLR model excluding 2 variables.
class : SpatialPointsDataFrame
features : 4756
extent : 182502.4, 290751, 340054.1, 450905.3 (xmin, xmax, ymin, ymax)
crs : +proj=tmerc +lat_0=4 +lon_0=8.5 +k=0.99975 +x_0=670553.98 +y_0=0 +a=6378249.145 +rf=293.465 +towgs84=-92,-93,122,0,0,0,0 +units=m +no_defs
variables : 9
names : status, distance_to_tertiary_road, distance_to_city, distance_to_town, water_point_population, local_population_1km, usage_capacity, is_urban, water_source_clean
min values : 0, 0.017815121653488, 53.0461399623541, 30.0019777713073, 0, 0, 1000, 0, Borehole
max values : 1, 10966.2705628969, 47934.343603562, 44020.6393368124, 29697, 36118, 300, 1, Protected Spring Iteration Log-Likelihood
=========================
0 -1959
1 -1680
2 -1531
3 -1447
4 -1413
5 -1413 gwr.fixed_1$y <- as.factor(gwr.fixed_1$y)
gwr.fixed_1$most <- as.factor(gwr.fixed_1$most)
CM_1 <- confusionMatrix(data = gwr.fixed_1$most, reference = gwr.fixed_1$y)
CM_1Confusion Matrix and Statistics
Reference
Prediction FALSE TRUE
FALSE 1833 268
TRUE 281 2374
Accuracy : 0.8846
95% CI : (0.8751, 0.8935)
No Information Rate : 0.5555
P-Value [Acc > NIR] : <2e-16
Kappa : 0.7661
Mcnemar's Test P-Value : 0.6085
Sensitivity : 0.8671
Specificity : 0.8986
Pos Pred Value : 0.8724
Neg Pred Value : 0.8942
Prevalence : 0.4445
Detection Rate : 0.3854
Detection Prevalence : 0.4418
Balanced Accuracy : 0.8828
'Positive' Class : FALSE
From the output, this GWLR model has a slightly better Accuracy of 0.8846 compared to that of the GWLR model with all variables included (0.8837). However since the difference in Accuracy is very minimal, we can conclude that the performance of the GWLR model is also not really impacted when two independent variables are excluded.
Visualising GWLR
Osun_wp_sf_selected <- Osun_wp_sf_clean %>%
select(c(ADM2_EN, ADM2_PCODE,
ADM1_EN, ADM1_PCODE,
status))gwr_sf.fixed <- cbind(Osun_wp_sf_selected, gwr.fixed)Visualising coefficient estimates
The code chunk below is used to create an interactive point symbol map.
tmap_mode("view")
prob_T <- tm_shape(Osun) +
tm_polygons(alpha = 0.1) +
tm_shape(gwr_sf.fixed) +
tm_dots(col = "yhat",
border.col = "gray60",
border.lwd = 1) +
tm_view(set.zoom.limits = c(8,14))
prob_Ttmap_mode("plot")Those darker coloured points represent the functional water points which predict the functional ones better than the non-functional ones. Whereas the light coloured points represent the non-functional ones which predict the non-functional ones better than the functional ones.